| 实验名称 | 形式语言和自动机 |
熟悉形式语言和自动机,设计程序实现有限自动机,学习对字符串进行合法性检测,使用有限自动机判断字符串是否是可以被接受的。书写出能够成功运行的代码。
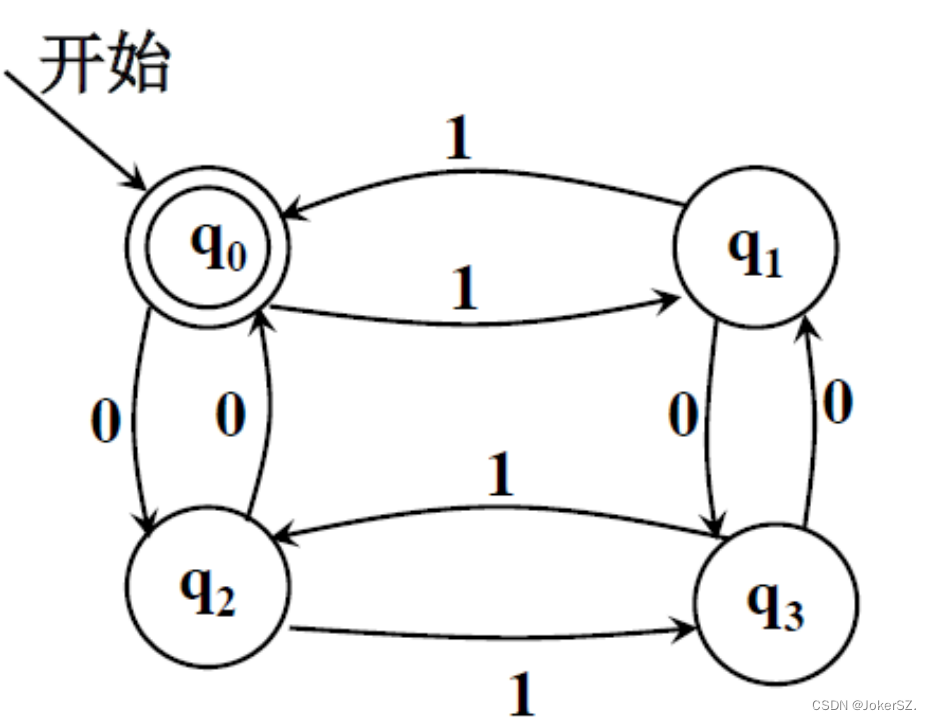
状态集为{ q0, q1, q2, q3 },输入符号集为{ 0,1 },初始状态为q0,终止状态为q0,在如下的状态转移函数中输入字符串,判断该字符串的合法性以及能否被接受。
输入:三行,每行一个字符串,询问能否被接受。 输出:三行,对于每一个输入,判断字符串合法性并由有限自动机判断是否可以被接受。
将状态图转化为二维数组,二维数组的第一维保存的是每个状态,也就是q0到q3,分别用0-3表示;第二维保存的是符号集,也就是转移的指标0、1;而数组的值表示的是转移后的状态。将所给的状态图转化为二维数组表示如下:
通过check()函数实现。依据之前创建的二维数组状态表,进行字符串中每个符号到相应状态的转化。通过a1和a2分别得到状态数组的一维和二维,由上述数组创建可知第一维保存的是每个状态,也就是q0到q3,分别用0-3表示;第二维保存的是符号集,也就是转移的指标0、1;整体通过for循环实现状态的转化。最终的状态通过a1的值得到。若最终返回状态q0,则a1最终的值为0。
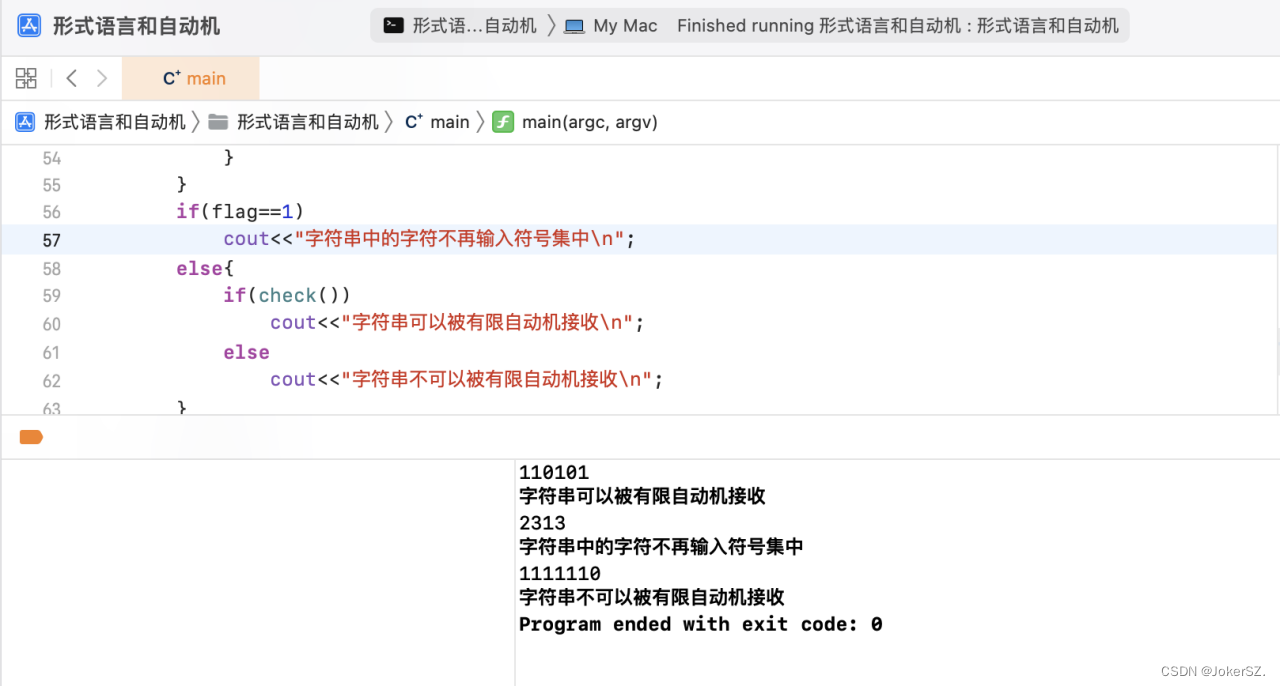
判断check()函数判断完成后进行输出:
通过此次形式语言和自动机的实验,我更加深刻的认识了有限自动机,掌握了有限自动机转换过程,熟悉了状态转移的具体过程以及代码实现方法,通过思考和状态转移的演示,想到了二维数组来存储状态图,编写代码过程中也逐渐发现二维数组可以实现。 | |
参考代码:
#include <iostream>
using namespace std;
int a[4][2];
int sum=0;
int q[100];
int check(){
int a1=0,a2;
for(int i=0;i<sum;i++)
{
a2=q[i];
a1=a[a1][a2];
}
if(a1==0)
return 1;
else
return 0;
}
int main(int argc, const char * argv[]) {
// insert code here...
int flag=0;
int i=0,j=0;
int ch;
a[0][0]=2;
a[0][1]=1;
a[1][0]=3;
a[1][1]=0;
a[2][0]=0;
a[2][1]=3;
a[3][0]=1;
a[3][1]=2;
while(i<3){
cin>>ch;
int ch2=ch;
while(ch){
ch/=10;
sum++;
}
for(j=sum-1;j>=0;j--)
{
q[j]=ch2%10;
}
for(int i=0;i<sum;i++)
{
if(q[i]!=0&&q[i]!=1)
{
flag=1;
}
}
if(flag==1)
cout<<"字符串中的字符不再输入符号集中\n";
else{
if(check())
cout<<"字符串可以被有限自动机接收\n";
else
cout<<"字符串不可以被有限自动机接收\n";
}
flag=0;
i++;
}
return 0;
}